Almost a century ago, Albert Einstein developed his most fantastic successful theory of physics ever - that of general relativity. What is likely the most important (from Einstein's perspective) facet of this theory is that gravitational information on the position of masses is not instantly available throughout the universe but rather travels from one point to another at the speed of light. Today, scientists around the world are using cutting edge technology both for theoretical development and physical detection of the gravitational radiation which transmits not only gravitational information but also energy and angular momentum. With many of the recent successes we've seen on both the theoretical and observational side of the problem, the next decade is an exciting time for relativists (those who study general relativity) as the first direct tests of this key result, and perhaps the first direct detection of black holes, will come to fruition. The object of this presentation (both as a blog and the talk I am developing) will be to explain what are gravitational waves, how we intend to detect them, and the efforts to better understand the underlying theory that produces these gravitational waves.
A Whole Other Spectrum.

In a classical sense, radiation is the process of transporting energy through a medium from one point to another without actually moving some amount of matter between the two points. Sound is a form of radiation represented by a compression of the air that is transmitted, perhaps from someone's mouth to a person's ear. Physicists most often deal with electromagnetic radiation. These are waves that show up in the electric and magnetic fields that propagate through space at the speed of light. Light, gamma-rays, x-rays, ultraviolet, infrared, radar and all the bandwidths by which we communicate such
 as TV and radio signals are parts of the electromagnetic spectrum. The primary parameter of electromagnetic radiation is the wavelength, the separation in distance between high points in the wave, or inversely, the frequency, the number of time a wavelength passes a given point in a second. My second diagram shows a wavelength. Multiplying the two together, the wavelength and frequency of electromagnetic radiation, you always get the speed of light. Key to my argument though is the idea of a spectrum. In the case of electromagnetic radiation, the electromagnetic spectrum is all the possibilities of wavelength the radiation can have, whether it be visible light or any of the other ranges I listed above. Einstein's General Theory of Relativity allows for a similar effect when considering the treatment of gravity - that there can be energy radiated from a source at the speed of light. However, I am not simply going to ask you to just believe me when I say this. I will provide a basic argument supporting this claim for gravitational radiation.
as TV and radio signals are parts of the electromagnetic spectrum. The primary parameter of electromagnetic radiation is the wavelength, the separation in distance between high points in the wave, or inversely, the frequency, the number of time a wavelength passes a given point in a second. My second diagram shows a wavelength. Multiplying the two together, the wavelength and frequency of electromagnetic radiation, you always get the speed of light. Key to my argument though is the idea of a spectrum. In the case of electromagnetic radiation, the electromagnetic spectrum is all the possibilities of wavelength the radiation can have, whether it be visible light or any of the other ranges I listed above. Einstein's General Theory of Relativity allows for a similar effect when considering the treatment of gravity - that there can be energy radiated from a source at the speed of light. However, I am not simply going to ask you to just believe me when I say this. I will provide a basic argument supporting this claim for gravitational radiation.Maxwell's Equations
 Presented to the left are Maxwell's equations. For now, all I want to say is they are a set of four linear differential equations that fully describe the behavior of the electric and magnetric fields. What is more important to me, however, is a certain result that can be obtained from these equations: the wave equation. Given a certain coordinate choice and in the absence of charge, the equation below can result. There are a couple of details that if I don't mention, some engineer might take issue with me. First, I have eliminated any constants dealing with the velocity of the wave and second, I have written the equation in an uncommon form. This is because I want you to focus on the part in the parenthesis. The object in the parenthesis is known in mathematical communities as the wave operator because the solution to that operator is the mathematical solution for a wave. When a wave operator acts on a field, the solution to that field i
Presented to the left are Maxwell's equations. For now, all I want to say is they are a set of four linear differential equations that fully describe the behavior of the electric and magnetric fields. What is more important to me, however, is a certain result that can be obtained from these equations: the wave equation. Given a certain coordinate choice and in the absence of charge, the equation below can result. There are a couple of details that if I don't mention, some engineer might take issue with me. First, I have eliminated any constants dealing with the velocity of the wave and second, I have written the equation in an uncommon form. This is because I want you to focus on the part in the parenthesis. The object in the parenthesis is known in mathematical communities as the wave operator because the solution to that operator is the mathematical solution for a wave. When a wave operator acts on a field, the solution to that field i s a wave solution. In this case, the wave operator acts on the electric field, implying the solutions to the electric field will have wave properties. The result is similar for the magnetic field and thus we say, Maxwell's equations admit electromagnetic radiation. Most important to remember, however, is that when you see the wave operator (the part in the parenthesis) you should think the result is a wave-solution.
s a wave solution. In this case, the wave operator acts on the electric field, implying the solutions to the electric field will have wave properties. The result is similar for the magnetic field and thus we say, Maxwell's equations admit electromagnetic radiation. Most important to remember, however, is that when you see the wave operator (the part in the parenthesis) you should think the result is a wave-solution.
Causality
Causality is why the wave operator is so important. It is a mathematical representation of causality: the idea that events are chain together such that information about a change made in one place propagates down the line to reach another place by a moving change in the relevant field (a wave). If you look at the wave operator (the part in the parenthesis), there are two parts, both of which are called partial derivatives. A derivative measures how a quantity changes as you vary the relevant variable. If you look at the equation I have written, the first part is related to change as the time of measurement is varied while the second measures a change related to the change in the position of the measurement. Subtracting these relevant changes, I get zero. This suggests that as the electric field goes through these changes in time, it so goes through these changes in space - the essence of causality.
Einstein spent a great deal of time contemplating causality. You see, in his time, we had a number of odd experiments that all showed that the speed of light seems to be measured the same no matter what speed you are going. This is a very odd concept compared to the world we are used to dealing with. If I am traveling at thirty miles per hour on the road and someone else passes me at thirty-five miles per hour, I see them traveling at five miles per hour. These are the physics we are used to however, when we measure the speed of light, no matter the case, we measure 299,800,000 meters per second. This means it takes light about eight and a half minutes to reach Earth from the Sun. What Einstein theorized and we have later tested is that when two people have very different relative speeds, they actually measure distance differently. Again this does not seem very intuitive. This does not occur in the world in which we live. The key which makes this seem not unreasonable is that this effect is only measurable at very high relative speeds. However, I have yet to get to the most amazing part. The natural question to ask is if two people measure the distance between the same two points and get different values, which one is right? The correct answer is both of them! Key to any theory of relativity is that there is no preferred reference frame and that is exactly why we must measure the speed of light the same no matter what speed we are traveling at.
A result of this line of thinking was about information. Information is exactly what you'd think. Information exists on the position, mass and various other attributes of objects. Let's say an electron is at a given position x=0 in space. Let's then say it moves to a new position x=1 in space. To an observer a some distance from this event, the way to measure this change is by measuring the change in the electric field. That change in the electric field provides the observer with the information with which they can infer the change in position of the charge. The change in the electric field occurs via an electromagnetic wave which propagates out in all directions and gets to the observer at the speed of light. Thus if one imagined the sun would cease to exist, we'd learn of that here on Earth eight and half minutes later, the time it takes light to reach the Earth. Einstein generalized this idea by saying that no information can travel faster than the speed of light. In fact, that information can't travel faster than the speed of light is the core of relativity, not necessarily the speed of light itself.
A funny thing happens when you look at the theory of gravity in this light. Below, I have Newton's equation for the force of gravity between two objects. The capitol G is a constant, the two Ms refer to the masses of the individual objects and the r refers to the distance between them. Looking at this equation, it would seem that the instance a massive object moved, information about th at move would be instantly available to another by measuring the change in the force of gravity. Clearly, if it is true that information can't travel faster than the speed of light, if causality as we understand it today is to have meaning at all, Newton's theory of gravity most not be telling the whole story. This was the problem Einstein had in mind when he set about developing his most amazing theory yet - the General Theory of Relativity.
at move would be instantly available to another by measuring the change in the force of gravity. Clearly, if it is true that information can't travel faster than the speed of light, if causality as we understand it today is to have meaning at all, Newton's theory of gravity most not be telling the whole story. This was the problem Einstein had in mind when he set about developing his most amazing theory yet - the General Theory of Relativity.
Gravity is Curvature (not a force).
To address this issue of gravity not conforming to the concept of causality, Einstein made use of his extensive mathematical knowledge. He looked at the concept of Riemannian geometry. Those knowledgeable about a great deal of mathematics will know the name Riemann. His work focused on all sorts of fields of applied and theoretical mathematics. In particular, Einstein was interested in definitions of curvature within a given space. He found that if you treat time as a dimension like space, you can actually relate the curvature of the combined space-time to the distribution and movement of energy and mass. Further, he said that the movement of energy and mass is determined by geodesics of that curvature. These two ideas are represented by the equations to the left. On the left side of the first equation, you see a capital G with two indices to the bottom right of it. That G is called the Einstein tensor and represents a measurement of the curvature of space time. The indices mu and nu each go from zero to three. A tensor can often be represented as a matrix and in this case, it is a four by four matrix. The zero components are related to time and the one through three components represent the three spatial dimensions we are used to. On the right hand side you see a capitol T which is the stress energy tensor. It represents the distribution and flow of mass and energy. As such, the first equation represents the curvature of space being determined by the distribution of mass and energy. The second equation is called the equation of the geodesic. In a space where the curvature is not zero, there are no straight lines. Imagine drawing a line along the surface of a ball. That line won't truly be straight. The first term in the equation is the acceleration of a particle (an x with two dots above it). The x's with a single dot represent the velocity of a particle. The other character (the capital gamma) is derived from the shape of the space. This equation, then determines the path a particle will take in the absence of forces in curved space. In the presence of forces, a term would be entered on the right side of the equation to represent that force. So putting the two statements together, we have, the position and flow of energy and mass determines the shape of space and the shape of space determines the position and flow of energy and mass. These concepts are not simple and I will discuss them in more detail in the next two sections.
and mass is determined by geodesics of that curvature. These two ideas are represented by the equations to the left. On the left side of the first equation, you see a capital G with two indices to the bottom right of it. That G is called the Einstein tensor and represents a measurement of the curvature of space time. The indices mu and nu each go from zero to three. A tensor can often be represented as a matrix and in this case, it is a four by four matrix. The zero components are related to time and the one through three components represent the three spatial dimensions we are used to. On the right hand side you see a capitol T which is the stress energy tensor. It represents the distribution and flow of mass and energy. As such, the first equation represents the curvature of space being determined by the distribution of mass and energy. The second equation is called the equation of the geodesic. In a space where the curvature is not zero, there are no straight lines. Imagine drawing a line along the surface of a ball. That line won't truly be straight. The first term in the equation is the acceleration of a particle (an x with two dots above it). The x's with a single dot represent the velocity of a particle. The other character (the capital gamma) is derived from the shape of the space. This equation, then determines the path a particle will take in the absence of forces in curved space. In the presence of forces, a term would be entered on the right side of the equation to represent that force. So putting the two statements together, we have, the position and flow of energy and mass determines the shape of space and the shape of space determines the position and flow of energy and mass. These concepts are not simple and I will discuss them in more detail in the next two sections.
Wait, Curvature?
Curvature can be a difficult topic to understand. As an aide, I have put a diagram of a globe to the side. Around the middle of the globe is the equator. Imagine someone starting at the point marked A with an arrow pointed northward. That person then travels to the north pole all the while holding the arrow in the same direction. As you can see, at this point the arrow is now pointed south. If that person then walks to his right without changing the way he is holding the arrow to the equator, the arrow is no longer pointing south. If he then walk along the equator back to his original position, without changing the direction he is holding the arrow, when he arrives back at his starting position, the direction the arrow is being held is different than when he started. As you can see on my diagram, the angle between the starting orientation and the final orientation of his arrow is represented by alpha. A non-zero alpha represents a non-zero measurement of curvature of the space. The key here is that the person at no point changed the way he held the arrow, simply walking in a set path to get back to his starting position. This is a kind of curvature we can measure from within a system and it is that curvature that is represented by the capital G (the Einstein tensor) above.
Now you know we can measure curvature but we can also need the idea of parallel transport or geodesic motion. In a curved space, an object without a force acting on it will rather travel on a geodesic since straight lines are available. To the left I have another drawing of a glob and this time I would like to start two people off on the equator, one at point A and one at point B. They both then travel directly north. Initially, they are traveling in parallel lines (both travelling north from the equator). However, looking at the drawing we find that their paths intersect at the north pole. With curved spaces, to parallel paths can be drawn together in the absence of any force if their geodesics (the preferred path given the geometry) brings them together as we saw in the drawing.
Using Curvature to Describe Gravity
With this understanding of curvature in hand, we'll move on to how this relates to gravity. If you take time as a dimension, just like spatial dimensions, you then get what we call a space-time. If you then think of an observer (say a person or a particle) as having a four-velocity rather than a three velocity, that four-velocity behaves according to the equation of the geodesic. What that means is there becomes some (arbitrary) parametrization of space-time and any equation which describes a path through that space time, in the absence of forces obeys the equation of the geodesic. So if we are moving through time, just like the two arrows come together on my second drawing of a globe, so two does curvature bring two bodies spatially together. The other side of that is Einstein's equations which related the curvature of space-time (via the Einstein tensor) to the position and movement of mass and energy (via the stress-energy tensor). So like I said two sections ago, the distribution and movement of mass and energy determine the curvature of space and the curvature of space determines the distribution of and movement of mass and energy.
This is Einstein's theory of General Relativity and it is this theory which has led to some wondrous results. Gravitational lensing is used today to view galaxies from almost fifteen billion light-years away. This effect has allowed us to peer back to some of the earliest times in the history of the universe and is predicted by the understanding that the path of light is affected by the curvature of space-time. Black-holes where the gravity overcomes the forces holding up the structure of a star creates singularities inside event horizons which causally remove one part of space-time from another. Corrections from General Relativity have even been used in GPS systems improving their accuracy from a couple of yards to a couple of inches. A key result, however, is that of gravitational radiation, which transmits energy, angular-momentum and gravitational information from one point to another at the speed of light and which is what we are tyring today to understand and detect. This gravitational radiation is one of the key reason's Einstein set about developing General Relativity.
From GR to Gravitational Waves.
So we've now decided that gravity is the curvature of space-time which is great and has some interesting effects, some of which we have verified through observation and experiment. However, we've yet to see how GR maintains causality as I described above which is why I want to return to Einstein's equations (that thing with the G and the T). If you remember the G, the Einstein tensor, represents part of the curvature of space-time. As my next equation shows, the Einstein tensor is a function of something we call the metric represented by a lower cas e g. The metric defines the distance between any two points and contained within the metric is all the information about the curvature of space-time. My next equation takes this metric and breaks it into two parts that sum to the metric. The first part is represented by the Greek character eta and is what we call the flat-space metric. Flat-space is space like you are used to dealing with where the length of your meter stick remains one meter no matter what. In curved space, this meter stick can be stretched as different points on the meter stick are bent differently to the curve of space. The non-flat portion of the conformal metric is then represented by the lower case h. This part measures the effects of gravity that we interpret as a force in our everyday lives. Without going through the mathematics (and people in the field will agree with me), if you assume that h is small compared to eta and you use that assumption in the context of Einstein's equations without any matter in them, you arrive at an interesting result shown in my third equation of this section. What you should recognize is the wave operator acting on h. Well, you'll really see the wave operator acting on a projection of h. That TT on it stands for transverse and traceless (in case there are any mathematicians reading this). For the purpose of this discussion, that means it's a special way of looking at h. I've made other assumptions here to simplify the math but aren't really worth going into. Einstein's theory of general relativity has recovered a wave-operator in gravity. This means that information travels at the speed of light through gravitational waves that carry both energy and angular momentum and is exactly the result Einstein was looking for. I turns out gravitational waves similarly take about eight and a half minutes to travel the space between the Earth and the sun also and so if we again imagined the Sun were to suddenly disappear, we'd learn of it gravitationally in the same eight and a half minutes as we do by the light ceasing to arrive.
e g. The metric defines the distance between any two points and contained within the metric is all the information about the curvature of space-time. My next equation takes this metric and breaks it into two parts that sum to the metric. The first part is represented by the Greek character eta and is what we call the flat-space metric. Flat-space is space like you are used to dealing with where the length of your meter stick remains one meter no matter what. In curved space, this meter stick can be stretched as different points on the meter stick are bent differently to the curve of space. The non-flat portion of the conformal metric is then represented by the lower case h. This part measures the effects of gravity that we interpret as a force in our everyday lives. Without going through the mathematics (and people in the field will agree with me), if you assume that h is small compared to eta and you use that assumption in the context of Einstein's equations without any matter in them, you arrive at an interesting result shown in my third equation of this section. What you should recognize is the wave operator acting on h. Well, you'll really see the wave operator acting on a projection of h. That TT on it stands for transverse and traceless (in case there are any mathematicians reading this). For the purpose of this discussion, that means it's a special way of looking at h. I've made other assumptions here to simplify the math but aren't really worth going into. Einstein's theory of general relativity has recovered a wave-operator in gravity. This means that information travels at the speed of light through gravitational waves that carry both energy and angular momentum and is exactly the result Einstein was looking for. I turns out gravitational waves similarly take about eight and a half minutes to travel the space between the Earth and the sun also and so if we again imagined the Sun were to suddenly disappear, we'd learn of it gravitationally in the same eight and a half minutes as we do by the light ceasing to arrive.
How do Gravitational Waves Work?
We have recovered the wave operator but we still don't have a full understanding of gravitational waves.  There are elements of the mathematics dealing with the difference between tensors and vectors and the nonlinear nature of Einstein's equations compared to the linear nature of Maxwell's equations that suggest that while we have evidence of gravitational waves, they don't behave exactly the same as electromagnetic waves. In this section, I will present a description of what is physically happening with this wave operator (mostly by analog to an effect in Newtonian gravity). Every first semester physics class discusses Newton's three laws of dynamics. These have to do with the effects of forces which can be summed linearly, that is, if I have two forces acting on an object, the net force is simply the sum of the two forces. So if you look at my first diagram in this section, I have two bodies at some distance from the object in question. In Newton's gravity (not the relativity we looked at before), the force between two bodies points from one to the other. As you can see, the object being pulled on on the right has two small arrows, one for each body on the left. The large arrow represents the sum of the two small arrows. The net force then pulls the object in question towards the left. As long as the body in question is suitably small, this diagram accurately represents the physics of the situation. However, if the object being acted on is an extended body, such as most things in our daily lives which don't occupy simply one point in space but rather take up some volume, this description becomes insufficient. In my second drawing, I have an extended body being acted on according to Newton's gravity by two gravitational bodies on the left. As you can see, there is still a net force to the left.
There are elements of the mathematics dealing with the difference between tensors and vectors and the nonlinear nature of Einstein's equations compared to the linear nature of Maxwell's equations that suggest that while we have evidence of gravitational waves, they don't behave exactly the same as electromagnetic waves. In this section, I will present a description of what is physically happening with this wave operator (mostly by analog to an effect in Newtonian gravity). Every first semester physics class discusses Newton's three laws of dynamics. These have to do with the effects of forces which can be summed linearly, that is, if I have two forces acting on an object, the net force is simply the sum of the two forces. So if you look at my first diagram in this section, I have two bodies at some distance from the object in question. In Newton's gravity (not the relativity we looked at before), the force between two bodies points from one to the other. As you can see, the object being pulled on on the right has two small arrows, one for each body on the left. The large arrow represents the sum of the two small arrows. The net force then pulls the object in question towards the left. As long as the body in question is suitably small, this diagram accurately represents the physics of the situation. However, if the object being acted on is an extended body, such as most things in our daily lives which don't occupy simply one point in space but rather take up some volume, this description becomes insufficient. In my second drawing, I have an extended body being acted on according to Newton's gravity by two gravitational bodies on the left. As you can see, there is still a net force to the left.  However, if you consider the top and bottom parts of the extended body separately, you'll locally get different forces, the top part pulled little more in the upward direction and the bottom part pulled a little more in the downward direction. While the amount pulling the top up and the bottom down is small compared to the net force pulling the whole object to the left, it does cause a stretching effect such that the object will be elongated in the up and down direction. Now if you consider these two objects on the left to be orbiting each other, as they rotate, the direction of this stretching will also change. This constant stretching will put energy into our extended object on the right as it is being pulled in different directions. That energy comes from the separation between the two rotating bodies at the left. As energy goes into the extended object on the right, the distance between the objects at the left would shrink. In Newtonian gravity this reaction is immediate and does not obey causality. Further in Newtonian gravity, if there were no extended object on the right, no energy would be lost from the orbit of the two bodies at the left. In Einstein's theory of relativity, the extended body is irrelevant as energy is radiated away into the curvature of space-time purely by virtue of the two bodies orbiting each other.
However, if you consider the top and bottom parts of the extended body separately, you'll locally get different forces, the top part pulled little more in the upward direction and the bottom part pulled a little more in the downward direction. While the amount pulling the top up and the bottom down is small compared to the net force pulling the whole object to the left, it does cause a stretching effect such that the object will be elongated in the up and down direction. Now if you consider these two objects on the left to be orbiting each other, as they rotate, the direction of this stretching will also change. This constant stretching will put energy into our extended object on the right as it is being pulled in different directions. That energy comes from the separation between the two rotating bodies at the left. As energy goes into the extended object on the right, the distance between the objects at the left would shrink. In Newtonian gravity this reaction is immediate and does not obey causality. Further in Newtonian gravity, if there were no extended object on the right, no energy would be lost from the orbit of the two bodies at the left. In Einstein's theory of relativity, the extended body is irrelevant as energy is radiated away into the curvature of space-time purely by virtue of the two bodies orbiting each other.  Overall the effect of gravitational waves can be seen as my third diagram in this section. As the gravitational pull rotates, stretching and shrinking occurs similar to the pattern shown.
Overall the effect of gravitational waves can be seen as my third diagram in this section. As the gravitational pull rotates, stretching and shrinking occurs similar to the pattern shown.
You may have noticed in that diagram that there are two rows showing the effects on a given body. In one, the stretching occurs up and down and then left and right. In the second row, the stretching occurs at the angle between the previous orientation. We refer to this as the polarization states of the radiation. Through some combination of these polarization states, you can recreate the signature of any gravitational wave. For the mathematicians, physicists and engineers out there, these polarization states correspond to a spin-2 field. While my example was dependent on forces, the concept of the measurable effects of gravitational waves remains the same - the key difference being that like electromagnetic radiation (light, etc), an object picking up the changes isn't necessary for the corresponding effect on the source of the gravitational waves and so energy, information and angular momentum is still radiated out at the speed of light, whether we look at it or not. In the following sections, I will discuss what are real world sources of graviational waves and how we intend (on the most basic level) to detect this radiation.
Sources of Gravitational Waves
Technically speaking, a gravitational wave is caused by a asymmetric change in the position of a massive body. The asymmetry is important. Gravitationally speaking, if two objects are spherical, have the same mass but don't have the same size, I won't know the difference. Thus if something like a star grows and shrinks with perfect symmetry, the is no gravitational information to be found in gravitational radiation. It turns out, the universe is filled with massive bodies that move asymmetrically. 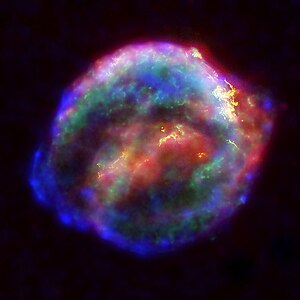 A good example is the Earth and the Sun. The Earth travels around the sun constantly producing a change in position. Similarly Jupiter's orbit is another example. These are relatively small objects however and so they emit little gravitational radiation (certainly not strong enough for detection any time soon). Naturally, we should start thinking big. Binary stars orbiting each other are another example with more mass. Stars are good but we've only found them to be as big as thirty times the mass of our Sun and while that's a lot of mass, they are not quite dense enough to produce gravitational waves we have a hope of detecting. The sources of gravitational waves we really expect to see are from Supernovae, neutron star and black holes - objects and events that pack a lot of matter in a small amount of space (standard jargon is to call these thing compact objects). A Supernova often emits a tremendous amount of energy all at once sending matter flying in all kinds of directions. Pictured is a remnant of a supernova. To put it in perspective, the original star would have been one point of light in this photo. A neutron star with the mass of the sun is so dense, it would take up less space than the Earth. Black holes are the most extreme. Black holes occur when the gravity in a star overcomes the forces holding it up and all the matter collapses into a singularity. When this occurs, an event horizon is created from which (barring quantum mechanical possibilities) nothing, not even light nor information, can escape. Some black holes are believed to be the heaviest individual objects in the universe, with the most massive examples being at the centers of galaxies. There they can range up to a million times the mass of the Sun. Due to their dense nature, these objects are some of the possible sources for gravitational waves we could most likely detect.
A good example is the Earth and the Sun. The Earth travels around the sun constantly producing a change in position. Similarly Jupiter's orbit is another example. These are relatively small objects however and so they emit little gravitational radiation (certainly not strong enough for detection any time soon). Naturally, we should start thinking big. Binary stars orbiting each other are another example with more mass. Stars are good but we've only found them to be as big as thirty times the mass of our Sun and while that's a lot of mass, they are not quite dense enough to produce gravitational waves we have a hope of detecting. The sources of gravitational waves we really expect to see are from Supernovae, neutron star and black holes - objects and events that pack a lot of matter in a small amount of space (standard jargon is to call these thing compact objects). A Supernova often emits a tremendous amount of energy all at once sending matter flying in all kinds of directions. Pictured is a remnant of a supernova. To put it in perspective, the original star would have been one point of light in this photo. A neutron star with the mass of the sun is so dense, it would take up less space than the Earth. Black holes are the most extreme. Black holes occur when the gravity in a star overcomes the forces holding it up and all the matter collapses into a singularity. When this occurs, an event horizon is created from which (barring quantum mechanical possibilities) nothing, not even light nor information, can escape. Some black holes are believed to be the heaviest individual objects in the universe, with the most massive examples being at the centers of galaxies. There they can range up to a million times the mass of the Sun. Due to their dense nature, these objects are some of the possible sources for gravitational waves we could most likely detect.
How are we going to detect gravitational waves?
The answer is interferometry. This is actually a pretty in depth technique. The basic concept is one of interference. Interference is what occurs when two waves exist in the same place. I'll start with constructive interference.  If you look at my first picture in this section, you'll see on the left two waves that are approaching each other. On the right, you'll see them when they are in the same place. The green shows the resultant pattern. When they add like this, it's called constructive interference. It creates a greater intensity.
If you look at my first picture in this section, you'll see on the left two waves that are approaching each other. On the right, you'll see them when they are in the same place. The green shows the resultant pattern. When they add like this, it's called constructive interference. It creates a greater intensity.  In my second picture, you'll see a similar situation except that the waves cancel with each other. This is called destructive interference. These are the effects of simple constructive and destructive interference and holds for all waves. In particular, I am interested in the effects of interference in light. There is a common physics experiment used in many college classes where light from a laser is beamed at two slits in a piece of cardboard.
In my second picture, you'll see a similar situation except that the waves cancel with each other. This is called destructive interference. These are the effects of simple constructive and destructive interference and holds for all waves. In particular, I am interested in the effects of interference in light. There is a common physics experiment used in many college classes where light from a laser is beamed at two slits in a piece of cardboard.  Behind this "double-slit" a ways is a white sheet of paper. What is interesting is what lights appears on the paper. My third picture is a diagram of this "double-slit experiment". The result is an interference pattern shown on the right of this diagram. Where the light waves interfered constructively, the light appears more intense and where the light waves interfered destructively, the light is almost non-existent. This is caused because the light is effectively being emitted in a regular pattern from the points b and c. As you can see in the diagram, this leads to the waves lining up differently and giving this interference pattern. Interferometry takes advantage of this effect to measure small changes in distance.
Behind this "double-slit" a ways is a white sheet of paper. What is interesting is what lights appears on the paper. My third picture is a diagram of this "double-slit experiment". The result is an interference pattern shown on the right of this diagram. Where the light waves interfered constructively, the light appears more intense and where the light waves interfered destructively, the light is almost non-existent. This is caused because the light is effectively being emitted in a regular pattern from the points b and c. As you can see in the diagram, this leads to the waves lining up differently and giving this interference pattern. Interferometry takes advantage of this effect to measure small changes in distance.
Interferometry
A laser emits a tight beam of phase aligned light. That means the waves in the light line up perfectly so that they constructively interfere. If you imagine that beam of light being split into two paths and later recombined, if one path were longer than the other, that would change the way the waves line up. It would change the interference pattern.  This is the key idea of interferometry. I have a diagram of an interferometer here. In this diagram a beam of light is emitted from a coherent light source. The "half-silvered mirror" splits the beam onto two paths with a mirror at their ends. The split beams travel down these arms, are bounced back and recombined into one beam directed at a detector. If one arm is longer than the other, the detector gets a different interference pattern which can be used to measure the difference in distance. Now think about my description of how gravitational waves work above. A gravitational wave stretches objects in a regular pattern. If such stretching occurs on an interferometer, the length of the arms would change in a regular pattern and be found in the detector. Now that I've put that out there, I should say it's easier said than done. If gravity were a force, it would be the weakest. We all know gravity so well because we live on such a big planet. In reality, an electron has a much bigger effect on the electromagnetic field than it does on the gravitational field. It just so happens that electrons tend to be paired with oppositely charged protons and so we don't notice their effects as much in everyday life. There is no such pairing in gravity. I bring this all up to express the immense difficulty in actually detecting gravitational waves. I'll go into specific projects next but for now I'll say this, we are building interferometers with five kilometer arms and we are expecting to pick up gravitational radiation with effects on the interference pattern smaller than the size of an atom.
This is the key idea of interferometry. I have a diagram of an interferometer here. In this diagram a beam of light is emitted from a coherent light source. The "half-silvered mirror" splits the beam onto two paths with a mirror at their ends. The split beams travel down these arms, are bounced back and recombined into one beam directed at a detector. If one arm is longer than the other, the detector gets a different interference pattern which can be used to measure the difference in distance. Now think about my description of how gravitational waves work above. A gravitational wave stretches objects in a regular pattern. If such stretching occurs on an interferometer, the length of the arms would change in a regular pattern and be found in the detector. Now that I've put that out there, I should say it's easier said than done. If gravity were a force, it would be the weakest. We all know gravity so well because we live on such a big planet. In reality, an electron has a much bigger effect on the electromagnetic field than it does on the gravitational field. It just so happens that electrons tend to be paired with oppositely charged protons and so we don't notice their effects as much in everyday life. There is no such pairing in gravity. I bring this all up to express the immense difficulty in actually detecting gravitational waves. I'll go into specific projects next but for now I'll say this, we are building interferometers with five kilometer arms and we are expecting to pick up gravitational radiation with effects on the interference pattern smaller than the size of an atom.
LIGO
 LIGO stands for Laser Interferometer Gravitational Wave Observatory. There are actually two LIGO detectors, one built in Hanford Washington and the other in Livingston Louisiana. These are the latest and largest interferometers yet built and they've been built specifically for the task of detecting gravitational radiation. Reading about LIGO is equivalent to looking at a list of superlatives. LIGO makes the best vacuum on Earth along the arms the lasers go down. Some of the most effective shock-absorbing technology created is used in LIGO and it makes use of mirrors specially designed for the task at hand. LIGO hears things you wouldn't believe. LIGO takes notice when a truck is driving down the highway. At the Livingston site, there is a logging facilty nearby which adds to the noise picked up. All this has to be sorted out and acounted for before gravitational waves can be found. I won't go into too much detail but rather suggest to those interested to google LIGO. The first hit is the LIGO website. For now, I'll talk about the basics of what has been accomplished and what may be accomplished with LIGO in the future. Recently they managed to run LIGO under it's current design specifications. What that means is they were able to measure the intereference pattern in the detector to the theoretical level of precision that scientists working on the project believed could be possible so far. At this level of design sensitivity, it was unlikely that during it's science run, any noticeable gravity waves would be found. That science run has completed and there are many scientists around the world pouring over the data, making use of some of the most cutting edge software developed for this project. As of yet, I haven't heard a detection from that science run. What LIGO is heading for is called Advanced LIGO. Advanced LIGO will allow detections of gravitational waves over far more wavelengths and will be able to detect gravitational waves from sources over fifteen times further away than the initial LIGO. That means detections could be made from sources in an area over three-thousand times as large (it will come to a radius of about six hundred megaparsecs for most sources). Given current estimates of numbers and frequency of possible sources of gravitational radiation, detection with Advanced LIGO seems certain. At the very least, this project will give us new insights into the nature of gravity and our estimates of compact objects in the universe. Construction and development of Advanced LIGO starts early this year (2009) and is expected to be complete and operational sometime in 2013. Our theoretical models suggest we'll be able to detect binary neutron stars, neutron star-black hole binaries and binary black holes with a total mass about thirty times the mass of the Earth. This is very exciting for relativists but also poses some tough problems. For one, the most powerful sources of gravitational waves, the orbit of supermassive black holes with masses up to a million times the mass of the sun will be in frequencies LIGO can't detect. For another, to actually understand these gravitational waves, there is some intense theoretical work to be done. The rest of this post will be devoted to providing some understanding of those theoretical models.
LIGO stands for Laser Interferometer Gravitational Wave Observatory. There are actually two LIGO detectors, one built in Hanford Washington and the other in Livingston Louisiana. These are the latest and largest interferometers yet built and they've been built specifically for the task of detecting gravitational radiation. Reading about LIGO is equivalent to looking at a list of superlatives. LIGO makes the best vacuum on Earth along the arms the lasers go down. Some of the most effective shock-absorbing technology created is used in LIGO and it makes use of mirrors specially designed for the task at hand. LIGO hears things you wouldn't believe. LIGO takes notice when a truck is driving down the highway. At the Livingston site, there is a logging facilty nearby which adds to the noise picked up. All this has to be sorted out and acounted for before gravitational waves can be found. I won't go into too much detail but rather suggest to those interested to google LIGO. The first hit is the LIGO website. For now, I'll talk about the basics of what has been accomplished and what may be accomplished with LIGO in the future. Recently they managed to run LIGO under it's current design specifications. What that means is they were able to measure the intereference pattern in the detector to the theoretical level of precision that scientists working on the project believed could be possible so far. At this level of design sensitivity, it was unlikely that during it's science run, any noticeable gravity waves would be found. That science run has completed and there are many scientists around the world pouring over the data, making use of some of the most cutting edge software developed for this project. As of yet, I haven't heard a detection from that science run. What LIGO is heading for is called Advanced LIGO. Advanced LIGO will allow detections of gravitational waves over far more wavelengths and will be able to detect gravitational waves from sources over fifteen times further away than the initial LIGO. That means detections could be made from sources in an area over three-thousand times as large (it will come to a radius of about six hundred megaparsecs for most sources). Given current estimates of numbers and frequency of possible sources of gravitational radiation, detection with Advanced LIGO seems certain. At the very least, this project will give us new insights into the nature of gravity and our estimates of compact objects in the universe. Construction and development of Advanced LIGO starts early this year (2009) and is expected to be complete and operational sometime in 2013. Our theoretical models suggest we'll be able to detect binary neutron stars, neutron star-black hole binaries and binary black holes with a total mass about thirty times the mass of the Earth. This is very exciting for relativists but also poses some tough problems. For one, the most powerful sources of gravitational waves, the orbit of supermassive black holes with masses up to a million times the mass of the sun will be in frequencies LIGO can't detect. For another, to actually understand these gravitational waves, there is some intense theoretical work to be done. The rest of this post will be devoted to providing some understanding of those theoretical models.
One Little Problem
So, General Relativity suffices as a theory of gravity that yields the wave-operator - meaning there will be gravitational waves. Further, we have projects that we think are going to be able to detect gravitational waves. You might think we're set, but there is one small problem. That problem is the gravitational constant. This constant describes the strength of the gravitational interactions between objects and that number is incredibly small. When I claimed that Einstein's field equations yield the wave operator as I presented it above, I made the claim based on the assumption that the space-time was flat with a small perturbation. The result is true with the caveat that such waves only comes from relatively small objects and the resultant wave is relatively small. If you combine that with the small size of the gravitational constant, you get a gravitational waves that we aren't likely to detect. We think the most common gravitational wave to be detected by LIGO will come from circularly orbiting binary black holes in the range of ten to thirty solar masses (ten to thirty times the mass of the Sun). Further, we suspect those signals will only be detectable during the very last stages of the binary where the two black holes merge into one. This stage releases the strongest gravitational radiation and has the difficulty of not being easily approximated as flat space with a small perturbation. This has us arrive at the key theoretical problem for gravitational waves - understanding the physics when the gravitational fields are strong, the objects involved are quickly moving and there are few symmetries to take advantage of.
One might ask, why is this a problem? Why not just detect gravitational waves and figure from that what they should look like? It's a fair question to which I have two responses. The first is that for projects like LIGO to get detections at all, they need to know what they are looking for. The other answer is that we are not simply interested in the detection of gravitational waves. While GW detection is itself a great feat which tests and fundamental aspect of Einstein's general relativity, the work becomes more interesting when seen in a broader light. Say we get a detection. I'd then want to know where the source is. What's made these waves? Is it a binary black hole pair? If so, what are the masses of the black holes? Were they spinning before collision? What is the spin of the resultant black hole? Does this source of gravitational waves have any interesting effects of the other stuff around it. One recent theoretical finding suggest that binary black holes will result in a remnant black hole with a significant kick velocity afterwards. If one then considers the possibility of supermassive black holes at the centers of some galaxies, when two such galaxies collide, the two black holes could merge with a tremendous kick velocity actually leaving the galaxies behind. This could have some very interesting effects relevant to astronomy. To understand the answers to all these questions, we need a good theoretical understanding of the physics of the generation of gravitational waves.
To start with, one needs to understand the nature of the problem. Einstein's field equations are a set of ten coupled second order non-linear differential equations. In layman's terms that means they are really, really, really hard to solve. Many solutions make use of some assumption like slow-moving systems with weak interactions or spherical symmetry or axial-symmetry. These solutions are great and have taught us a lot but they don't model the systems likely produce gravitational waves we can detect. The word that makes it really hard is nonlinear. While some sets of nonlinear equations can be solved in general, this is a facet that creates some difficulty and inevitably, any general method of solving Einstein's equations finds someway to be rid of this non-linearity.
 To deal with the difficulties of solving these equations for sources of waves we are likely to detect, there are two common methods in use today. One is that of perturbative methods, where you assume space to be flat with a number of correction terms linearly added to the system. By solving for the first non-flat term before the second (and so forth), each term is the solution to what is effectively a linearized set of equations. This has some advantages. It's analytic, meaning the solutions for the correction terms are written out as equations and the parameters like spin and mass can be easily adjusted. When I assumed space to be flat with a small change above (where I set the metric to be equal to the eta-term plus an h-term), that was a first order perturbative solution. The equation here extends to higher order terms. This representation is a vast simplification but gets across the idea. There are still problems with this method. While these higher order perturbative terms increase the accuracy of the result, we are still on some level assuming small curvature and slow moving objects. Ultimately, these methods still don't completely describe the physics of the most astounding cases - where black holes merge. Knowing these limitations, there are still many things that can be learned from these methods and ultimately, the templates we develop to match against for gravitational waves will likely involve the solutions found through these methods with some level of tuning. To accurately deal with the merger of two black holes, one of the strongest possible gravitational events and most likely to be detected by LIGO, we generally turn to another tool - numerical relativity.
To deal with the difficulties of solving these equations for sources of waves we are likely to detect, there are two common methods in use today. One is that of perturbative methods, where you assume space to be flat with a number of correction terms linearly added to the system. By solving for the first non-flat term before the second (and so forth), each term is the solution to what is effectively a linearized set of equations. This has some advantages. It's analytic, meaning the solutions for the correction terms are written out as equations and the parameters like spin and mass can be easily adjusted. When I assumed space to be flat with a small change above (where I set the metric to be equal to the eta-term plus an h-term), that was a first order perturbative solution. The equation here extends to higher order terms. This representation is a vast simplification but gets across the idea. There are still problems with this method. While these higher order perturbative terms increase the accuracy of the result, we are still on some level assuming small curvature and slow moving objects. Ultimately, these methods still don't completely describe the physics of the most astounding cases - where black holes merge. Knowing these limitations, there are still many things that can be learned from these methods and ultimately, the templates we develop to match against for gravitational waves will likely involve the solutions found through these methods with some level of tuning. To accurately deal with the merger of two black holes, one of the strongest possible gravitational events and most likely to be detected by LIGO, we generally turn to another tool - numerical relativity.
Next: What is Numerical Relativity?
Thanks to Wookiee for suggesting the use of the time it takes light to get to the Earth as an example.




I'd invite anyone who looks at this to post questions and comments on anything they feel needs more explanation / needs a better explanation. Doing so will help me better develop this discussion and the talk I am developing to go along side this.
ReplyDeleteI've got to say, I kind of lost interest around "These are Maxwell's equations".
ReplyDelete"gravitational information on the position of masses is not instantly available" - so does this mean if we were to suddenly, say, remove the sun, its effect on the earth wouldn't be felt immediately, but rather since the gravity wave goes at the speed of light, the effect would be felt at exactly the moment we saw the sun disappear, even though the actual removal happened like 8 minutes ago?
This comment has been removed by the author.
ReplyDeleteYou shouldn't identify people on the internets.
ReplyDeleteSorry, I wasn't thinking. Comment was removed to comply.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDeleteDude this is awesome...took me a while to comprehend with leave in London and large amounts of booze getting in my way. Maybe I didn't read carefully enough still, but I'm confused about one thing. If gravity is not a force but curvature of space time, then why does information about it need to travel at light speed? If the sun disappeared, wouldn't Earth automatically fly off the hinge rather than waiting eight minutes to do so? No force, no causality, no waves? Is there a difference between gravity and information about it. I feel like you satisfactorily explained gravity by declassifying it as a force but then used used force-logic to describe it. If it's not a force, shouldn't it rather be a constant built into the three other forces?
ReplyDeleteAlso, with gravitational radiation, is this what Hawking means when he says information is retained in black holes and is this how it gets out?
Sorry if all of this sounds really dumb...thanks if you take time to respond to us simple folk! :-) Plus I'm scared that if you get mastery over of gravity it'll be a big advantage you'll have over me in universe domination.
I should say as physical laws go, that information can't travel faster than the speed of light is of a higher order than a given theory of gravity or than most scientific theories for that matter. This is a result we have never yet found to be incorrect and every way we look at it, it comes out the same. This idea is what led Einstein to create GR. When applying the idea to gravity as curvature, think of this mind game. Imagine a sheet stretched out. If I hold my finger down on one part of the sheet, a curvature is induced. If I then lift my finger, the sheet does not immediately go back to being flat but takes time for the effect to be felt everywhere. Thus, information about curvature travels at or below the speed of light. This is exactly why I specify information rather than light. Information is a far broader concept and it's technically more accurate to say that information can't travel faster than the speed of light than to say particles or light can't travel faster than the speed of light.
ReplyDeleteIn a sense, your question about gravity being built into the rest of the forces has some merit. If you look at my equation of the geodesic (the one with the 'x's and dots), that equation describes how a particle moves in the absence of force but in a curved spacetime. You know it is in the absence of forces because it equals zero. To add forces, I would simply replace the zero with the value of the force. So in a sense, you intuition about gravity being built in is right - however, as a relativist, I would see it exactly inverse of that! :-)
As to Stephen Hawking's recent public talk, he was discussing information in general (remember this should be regarded a a theory of a higher order) and the mechanism by which information is retrieved can be through gravitational radiation or through the three "real forces". While this isn't my field, I believe I have a cursory understanding of the problem (though don't quote me on this). If you imagine a spherical black hole and some matter falls into it, there is a great deal of information connected to that matter. Now we state that the interior of a black hole (inside the event horizon) is causally disconnected to the exterior (meaning the inside does not affect the outside). So it would seem that information is lost a matter falls into a black hole. Just as we tend to think information travels at the speed of light, we tend to also think information is preserved so it would seem ideas of matter falling into a black hole and ideas of the conservation of information are at odds with each other. However, as the matter falls into a black hole, the matter leaves a change in the shape of the event horizon. You could imagine individual particles leaving little bumps on the event horizon. These bumps would fade over time. My interpretation of what Hawking's said was that the information in these bumps is preserved and can be retransmitted - through both gravitational radiation and more traditional "force-based" radiation. Thus the existence of black holes does not conflict with the conservation of information.
Great questions!
Ugh, I just read my posted comment and my grammar is terrible. Sorry about that.
ReplyDelete